Computer programming is how we tell computers to do what we want. When asked if they know programming, most people will name programming language(s) if they know any. However, programming and programming languages are two distinct things. A program is a set of instructions that a computer understands, programming is the art of prescribing the logic of doing something in a clear, step-wise, structured fashion, whereas programming languages are like natural languages, they have a set of words and syntax rules. Most programs can be expressed in any of the computer languages, the choice of language depends on which language the programmer is fluent in, which language is understood better by the target computer, and some other factors like difficulty of programming vs the efficiency of the written program, etc. Programs can usually be translated from one language to other, just like human speech can be expressed in different natural languages. However, most of the main ideas, the logical structures, are same across majority of the languages. If you understand these, then you can write programs in any computer language, all you need is some reference material to that language which defines key words and syntax, just like we need dictionaries and grammar rules for natural languages.
One very important thing to remember is that computer programs are very unforgiving. If you say something obviously illogical to a person, they are likely to sense it and either ignore your mistake and assume the corrected sense, or ask you for clarification. But if you tell a computer something illogical, the computer is not intelligent enough to sense that, so it will just do what you ask. If you ask it to do something wrong, it will do it without questioning. Generally, the programming languages are also very strict about the spellings of the keywords and the syntax, whereas a person can normally understand if you do minor mistakes. But a computer will rather refuse to understand if you do a mistake that would be insignificant compared to how many mistakes we make while speaking or writing natural languages. It is in some ways similar to Legalese. So if you become good at logic and computer programming, it is quite likely that you will start to understand legal documents and legislation quite clearly as well. So let’s start learning programming in a bit different way than usual.
Main Parts of a Program
At the most basic level, from our perspective, there are four parts of a program, Input, Data Storage, Processing, and Output. If you think from the Processor’s perspective, main parts are Data and Instructions.
Input
A program will usually need some external input from one ore more sources, for example typed input from a user, digitised sound from a microphone, visual data from a camera, stored data from a hard disk, data communicated over the internet, etc. However, this isn’t essential, some programs can work without external input. These data types are quite different from our perspective, but for a computer, it must convert all of these data types to numbers, and that too in binary format, i.e. just zeros and ones.
Data Storage
Before we can do anything with the data acquired through some Input method, it must be stored somewhere. There are different types of storage options available, some are temporary, some are long-term, some are slow to access, some are fast. We choose one of these options depending on what we want to do with the data.
Processing
Processing involves manipulation of available data for Output. This data can be acquired externally as described above, or it can be hard-coded within the program. Main types of processing are Mathematical Operations, Iterations, Decisions based on Comparisons, and also taking care of Input and Output.
Output
Even though it’s technically possible to have a program without Output, it would be a pretty much useless program that would only consume energy and produce some heat from the processor. The Output can be of many types just like Input, for example, output to a screen, a printer, a speaker, a data storage device, some machine control, etc.
More on Data Storage
Data can be stored in Analogue format, like sound stored on cassette or gramophone record, and it can be stored in a digital format, like music on a flash drive. When we are talking about programming, data predominantly refers to digital data, and that too in a Binary Numbers format.
Understanding Binary Numbers
Consider a marble holder as shown below.

Let’s call this marble holder a Bit. When it’s empty, it represents Zero, and when it has a marble as shown below, it represents a One.

A single Bit can represent either a Zero, or a One. There is no other choice.
Now let’s consider two Bits placed side by side. When they are both empty, they represent a Zero, as shown below:

Now if we add a marble, we have the choice of putting it in the left Bit or the right Bit. But both have a different meaning. If we just wanted to add One, we would always put it in the right Bit, as below:

What if we want to add another One to these two Bits, to represent Two? We could put it in the left Bit, and if we ask someone how many marbles are there, they would say Two. But that’s straight counting of marbles, not a binary number representation. Why do we bother with the binary numbers? Why not just put as many marbles as the number we want to represent? It is not only possible, but that’s also how nature represents numbers in reality. For example, if nature wanted to represent the number Two Billion in hydrogen atoms, you will find two billion hydrogen atoms. Nature only deals with the numbers that are present in reality, whereas we are capable of using our imagination to think about numbers which are not actually present in front of us, or even when things are present in large numbers in front of us, we are unable to appreciate their exact quantities just by looking at them or touching them. Most people would struggle to appreciate quantities larger than 10 pieces. Some animals can appreciate larger numbers than we can. To cover our short-coming at instantly appreciating large numbers, we resort to an imaginary system of counting numbers, represented by words and symbols. This helps us count, and to imagine numbers without actually putting that many items in front of us. There are different counting systems, and binary number system is one of them. These systems follow strict rules so that when we communicate these numbers with each other, they mean the same thing to all of us. So in binary number system, when you want to add a One, you always put it on the right most side – but if the right most side already has a marble, then the rule is to move that marble one step to the left to mean that a One has been added, rather than actually adding another marble. This system allows us to represent much larger numbers than the actual marbles we have at hand. So let’s move the marble on the right one step to the left to represent previous One plus another One, totaling to Two:

Can we add One more to make it Three? Yes, according to the rule, we put a marble in the right most Bit, which is empty, to represent Three as below:

Can we add One more? Unfortunately we can’t. The right most Bit is already filled, we can’t move it to the left either because that Bit is also filled. So with just two marbles, we have been able to represent four numbers, 0, 1, 2, and 3. That is the limit of the binary system, you cannot represent more than 4 numbers with 2 marbles. What if we want to represent larger numbers than 3? We have to increase the number of marble holders and marbles to represent larger numbers. Let’s consider three empty bits to represent Zero now:

From the Two Bit example, we know how to get to number Three, so let’s jump to that first:
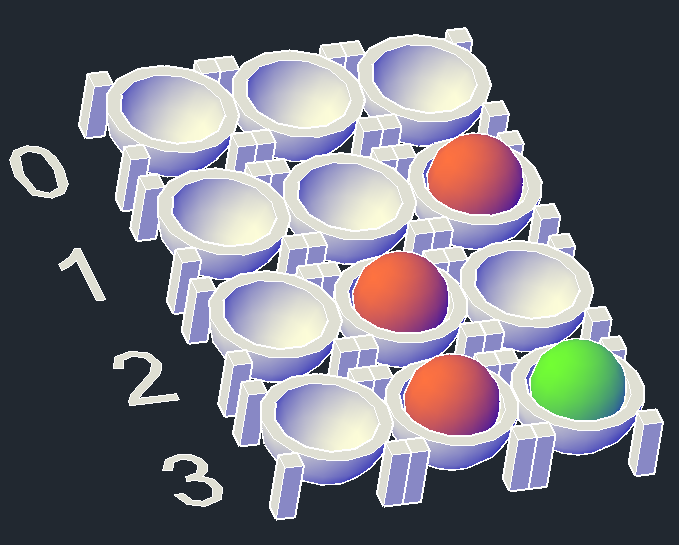
Earlier, when we had just two Bits, we could not count beyond 3, but now we have three Bits, can we add another One to Three, making it Four? Yes we can. So, to the right most Bit, we want to add a One, but since it’s already occupied, instead of putting a marble in that Bit, we empty it and move it to the left – but we can’t move it to the left in middle Bit because it’s also occupied. The same rule cascades, the the marble in the middle Bit moves to further left and leaves its place empty. So 4 appears is represented as below:

We can add more Ones the same way, until all the marble holders are filled, as below:
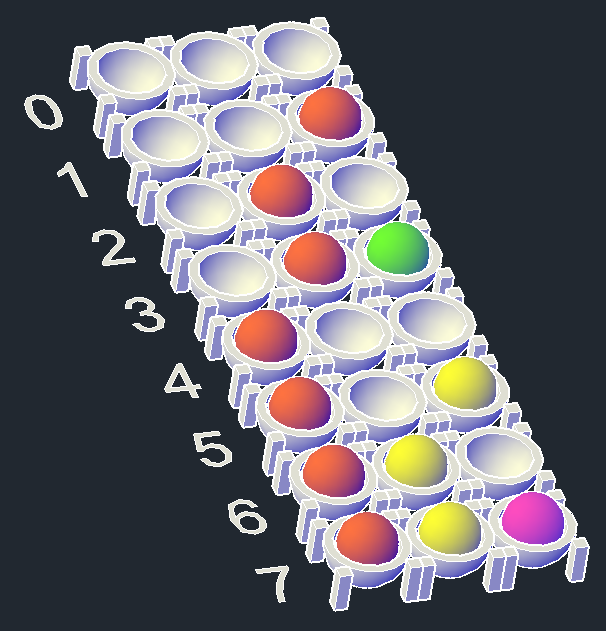
What you may have noticed is that when we had just one Bit, we could represent two numbers, when we added one Bit, we could represent four numbers, double than before. Then when we added the third Bit, the numbers we can represent has again doubled to eight. So, for every bit we add, the numbers we can represent doubles, as shown below:
| Number of Bits | Numbers that can be represented |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
| 7 | 128 |
| 8 | 256 |
The numbers in the above table are likely to sound familiar to you. For example, you may have come across 32-bit and 64-bit Windows or software, size of flash drives like 8GB or 64GB etc. Your mobile phone’s memory would also be represented by those numbers. So if you have ever thought why they are using such strange numbers instead of selling in 10GB, or 20GB, now you know the reason, it’s because electronic systems work in binary numbers. These numbers are as natural in binary number system as 10, 100, 1000, etc. are in decimal number system, the number system we use most frequently these days.
We also have a formula that can calculate the numbers we can represent with available bits as below:
n = number of bits
r = numbers than can be represented by n bits
r = 2n
Example:
n = 16
r = 216 = 65536
Why do we Use Binary Number System in Electronic Devices?
To be continued …
293 total views, 1 views today