In progress
Unit Prefixes
| Symbol | Prefix | Multiple |
| T | tera | 1012 (Multiply by 1,000,000,000,000) |
| G | giga | 109 (Multiply by 1,000,000,000) |
| M | mega | 106 (Multiply by 1,000,000) |
| k | kilo | 103 (Multiply by 1,000) |
| m | milli | 10-3 (Divide by 1,000) |
| μ | micro | 10-6 (Divide by 1,000,000) |
| n | nano | 10-9 (Divide by 1,000,000,000) |
| p | pico | 10-12 (Divide by 1,000,000,000,000) |
| f | femto | 10-15 (Divide by 1,000,000,000,000,000) |
Angles
Units
Angles are generally measured in Degrees (Degrees, Minutes, and Seconds) in practice. For use in engineering calculations, they are often converted to Radians. Degree units are an arbitrary measurement with no direct link with any units of measure for distance, which is why they don’t work in calculations. Radians are based Pi, which is based on the ratio of distance measurements, and it works with calculations. Other ways to represent angular measurements are slope and gradient. There’s one more system for angular measurement, the Gradians, or Gons, which I have never seen in practice except that the scientific calculators have the option to convert Degrees to Radians and Gradians. Apparently the French have been using it, and since 2020 the Gon has been given legal recognition in the EU and Switzerland.
Degrees
In this system, a circle is divided in 360 degrees, a right angle is 90 degrees and a straight line is 180 degrees. Each degree is divided in 60 minutes, and each minute is divided in 60 seconds. Further division of seconds is done in decimal units.
Symbol for a degree is ° , for minute ‘ and for second ” and the seconds can be written in decimal fractions.
Example: 63°44’5.345″
Decimal Degrees
We can also represent the degrees as decimal fractions, getting rid of minutes and seconds, which requires conversion.
For example, 63°44’5.345″ can be converted to decimal degrees as follows:
63 + 44/60 + 5.345/(60×60) = 63 + 0.73333333333 + 0.00148472222 = 63.73481805555

We can convert these decimal degrees back to d°m’s” by using the built in function of the calculator that comes with Microsoft Windows:
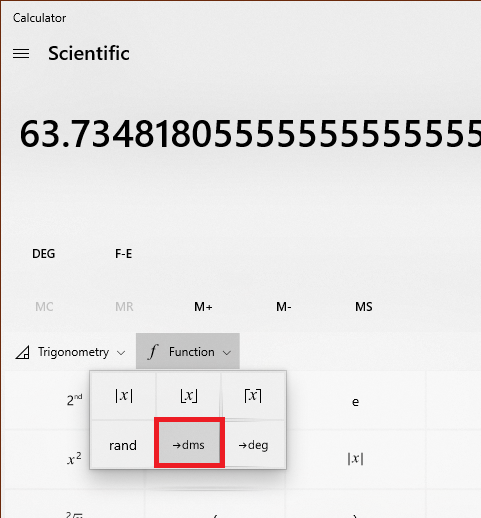
This gives us back the original degree minute second measurement as 63.4405345, which I consider to be not good enough these days. They could have used the actual symbols to separate the degrees, minutes and seconds rather than just separate degrees with a decimal point and then reserve 2 digits each for minutes and seconds. Even the decades old Casio calculators were using these symbols on seven segment displays.

Earlier we did the conversion from degree minute second format to decimal degrees by calculation, but on a scientific calculator, it can be done with build-in functions as well:
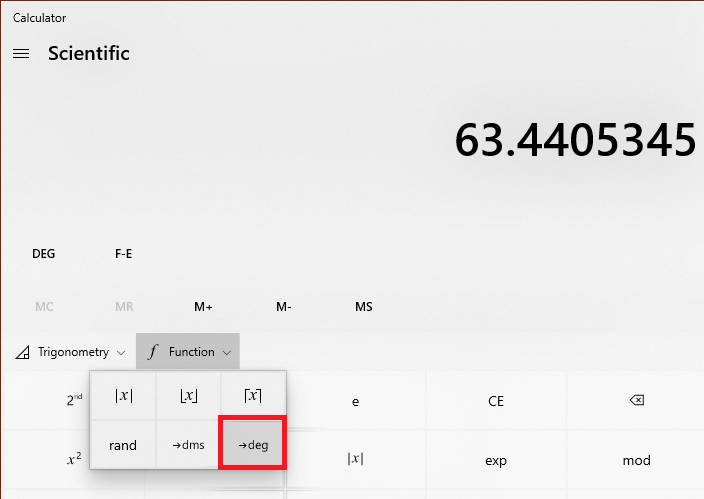
This quickly converts it decimal degrees:
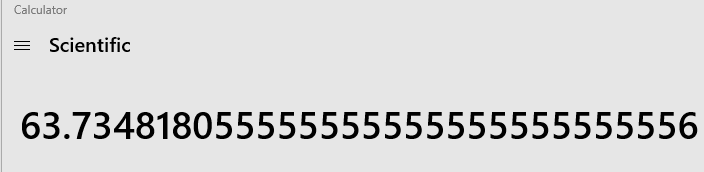
Microsoft Calculator has the DEG for degrees, RAD for radians and GRAD for gradians modes, which affect the trigonometric calculations, but it has no conversion function among these different units of angular measurement. This is nothing short of plain stupidity and ignorance. I believe the reason for this is that calculators in their electronic form are designed by engineers with experience of how the calculators are used by engineers and scientists, whereas the new Microsoft Calculator is made by people who do not have a good exposure to engineering and they probably just learned to write computer programs. It also shows the declining standards of education across the world. And this is not just with the Microsoft Calculator, they have also made the Microsoft Office worse than it used to be, many functions are missing from Microsoft Excel, and the new Equation Editor in Word isn’t as good as it used to be two decades ago.

Gradians/Gons
In this system, a circle is divided in 400 gradians, and a right angle is of 100 gradians or gons.
For conversion to degrees:
Decimal degrees = Gradians x 9/10
For conversion from degrees:
Gradians = Decimal degrees x 10/9
Radians
Radians are the only angular measurement units which are mathematically consistent with other measurements.
Then why don’t we just use Radians everywhere? Because they come up as fractional numbers based on Pi, which are not only harder to use and appreciate, but we also don’t get integer numbers for our commonly used angles such as 30°, 45°, 60°, 90° etc. So both ways have their own benefits, degrees are easier to measure and understand, whereas radians need to be used in calculations.
To be continued…
Current
Distance
Resistance
Time
Voltage
Volume
Weight
1,808 total views, 3 views today